構造謝爾賓斯基三角

關於謝爾賓斯基三角（Sierpinski triangle），是由波蘭數學家謝爾賓斯基在1915年提出的碎形圖案，最基本的構造方式是透過幾何來處理，而我在先前專欄文章〈遞迴、碎形與數學〉就談過作法：可以畫一個實心三角形，去掉邊長中點形成的三角形，接著針對新的小實心三角形、不斷重複以上的動作，之後就能夠產生謝爾賓斯基三角。

幾何／L-system／細胞自動機

使用程式碼描述謝爾賓斯基三角，顯得有點囉嗦，如果我們使用先前專欄〈碎形與L-system〉談過的L-system，此時，可以從公理（axiom）F-G-G出發，使用規則F->F-G+F+G-F與G->GG來衍生，等到衍生結束之後，以F替代G，最後依衍生出來的符號串——F是前進、+、-與左轉、右轉來繪圖，就能繪製謝爾賓斯基三角。

談到碎形，略為接觸過電腦繪圖的開發者，應該都會繪製碎形樹，例如，〈tree〉是我基於p5.js的碎形樹實作，那麼，你有辦法將碎形樹變成謝爾賓斯基三角嗎？其實，這並不困難，只要每次衍生三個分支，而分支之間的角度為120度，以及每次新分支會是上一次遞迴分支的一半長度，依此處理之後，就能得到謝爾賓斯基三角。

原理並不難理解，畢竟120度分支會構成正三角形，至於每次新分支是上一分支的一半長度，這不就是對應取三角形邊長一半的意思嗎？有興趣看看p5.js實作的人，可以參考我寫的〈TT Transformer〉。

對於直角座標，如果x座標、y座標使用(x?y)運算，其中的?，可以是+、-、*、/、^、&、|、%等運算子，將得到的數字在(x,y)處畫出來——圖片可參考〈x?y〉這則推文，我們即可觀察到謝爾賓斯基三角嗎？使用&運算而x&y為0的圖案就是了，在〈Matplotlib散佈圖〉裡的謝爾賓斯基三角，就是這麼畫出來的。

基於位元邏輯運算得到謝爾賓斯基三角，並不是偶然，而是一種細胞自動機的變化，我在先前專欄文章〈細胞自動機〉也談過，1983年英國電腦科學家Stephen Wolfram發表的基本細胞自動機（Elementary cellular automaton），在規則90時所畫出來的圖案，就是謝爾賓斯基三角。

巴斯卡三角／河內塔

謝爾賓斯基三角的構造方式如此多元，甚至可能藏在意想不到之處，例如，在巴斯卡三角裡，也隱含著謝爾賓斯基三角。我們可以試著將巴斯卡三角裡每個數字，繪製在一個圓（或方格），然後去掉2倍數的圓，就能得到謝爾賓斯基三角。

其實，我們也可以去掉巴斯卡三角裡3或4或5的倍數，這可以得到不同的圖樣，有興趣了解的人，可參考〈Pascal's Triangle Patterns〉。

或許跟謝爾賓斯基三角有著最神祕關係的，就是1883年法國數學家Edouard Lucas提出的河內塔吧！若有三個柱子、三個盤子，使用(abc)來表示小、中、大三個盤子，分別在a、b、c柱子，例如小中大盤都在1柱，就使用(111)代表當時河內塔的狀態，小中大盤各在2、1、1柱，就使用(211)表示，小中大盤各在3、1、1柱，就使用(311)。

由於(111)可以轉移至(211)或(311)，相對地，(211)、(311)都可以轉移至(111)，而(211)與(311)彼此間也可以轉換，若將可轉換的狀態間連線，能夠構成以下的三角形：

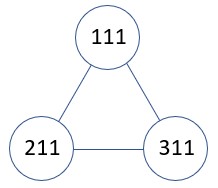
如果將河內塔全部的狀態轉換，依以上方式連線，構成的河內塔狀態轉移圖，就會是謝爾賓斯基三角；若有n個盤子，可以用n位數來表示從小至大的四個盤子，分別在哪個柱子上，例如，(2111)表示最小的盤子在2號柱，另三個盤子在1號柱……，那麼狀態轉移圖會變得更大，也就是得到一個更大的謝爾賓斯基三角，若你想看到呈現的形狀與關係的圖片，可參考〈河內塔〉。

混沌遊戲

如果想玩個不插電遊戲來畫出謝爾賓斯基三角，巴斯卡三角是個不錯的方式；另一種方式是丟骰子，首先點出三角形的三個頂點ABC，隨機在三角形內部選一點p0，然後開始丟骰子（如果得到1或2，選擇頂點A，3或4選B，5或6選C），在選擇的頂點與點p0間取中點畫出p1，繼續丟骰子，在選擇的頂點與點p1間取中點畫出p2，丟骰子，在選擇的頂點與點p2間取中點畫出p3……

如果努力不懈地丟骰子，畫出來的點會逐漸形成謝爾賓斯基三角的圖樣，我們可以在〈Chaos Game - Numberphile〉看到這個過程。其實，丟骰子只是個隨機選取頂點的過程，而這個不插電的遊戲稱為混沌遊戲（Chaos game）。

被稱為混沌的原因，是因為最初的點是隨機選取的，而每次也是隨機選取頂點，乍看似乎會得到個混沌不明的結果，最後卻得到了謝爾賓斯基三角。基本上，這個遊戲可以擴展至三維，使用第四個頂點構成正四面體，每次隨機選取四個頂點之一，其餘步驟同上，如此一來，就可以構成謝爾賓斯基四面體（Sierpinski Tetrahedron）。

其實，混沌之中並不完全是混沌，畢竟這裡隱含著每次迭代時的固定規則，若使用一般化來表示，對任一點進行pk，透過迭代函式f可得到pk+1點，也就是pk+1=f(pk)，這稱為迭代函式系統（iterated function system, IFS），而迭代函式系統是產生碎形的一種方式。

當然，在混沌中，並不是任何規則都會收斂成某個圖樣（或稱為狀態），例如，方才的玩法對於正方形的四個頂點，並不會產生碎形，然而，若我們試著在選取頂點時加些規則（或稱為限制），就有可能產生碎形（可參考維基百科〈Chaos game〉的圖片）。

如果混沌裡的規則（也就是迭代函式）可以收斂至某個狀態，該狀態被稱為迭代函式系統的吸引子（attractor）或不動點（fixed point）。對此，你是否想到類似的系統呢？我在先前專欄文章〈淺談反應擴散系統〉、〈實現差別生長演算〉談過的，就是類似的概念！

不同角度而息息相關

為何河內塔狀態轉移圖會出現謝爾賓斯基三角？關於數學上的道理，你可以參考〈Sierpinski Gasket and Tower of Hanoi〉；從另一角度來看，狀態轉移是自動機的範疇，而基本細胞自動機規則90可以繪出謝爾賓斯基三角，河內塔狀態轉移圖看似謝爾賓斯基三角，好像也就可以理解了。

類似地，混沌遊戲可以繪出謝爾賓斯基三角，也可以從數學上證明，有興趣可參考〈Chaos Game〉；或者應該說，碎形、自動機、混沌理論、人工生命、人工智慧等，都是彼此息息相關，從不同角度解釋某些現象的課題，能夠發現同一現象的不同構造方式，正是探索電腦科學最美妙的過程。