程式猴與基因演算法

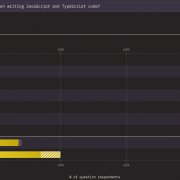
在不知道什麼樣的搜尋策略，可以找到最佳解時，若能善用基因演算法（Genetic Algorithm），可讓足夠好的方案，有更大機會將基因傳給下一代，最終自行演化出接近甚至等於最佳解的方案。

香蕉請到的猴子？

程式人很愛用猴子來嘲諷一些業界現象，例如程式猴（code monkey）常被用來形容只會依文件、書本、Stack overflow照抄程式而不知思考的傢伙，甚至有本書名為《軟體專案開發實務｜別只當編程猴》的書；另外，對於一些待遇與應徵資格不符的求才貼文，經常會得到「給香蕉只請得起猴子」之類的回應。

香蕉請到的猴子真的能用嗎？無限猴子定理（Infinite monkey theorem）指出：「讓一隻猴子隨機地在打字機上按鍵，若給予無限的時間，總有可能打出給定的任何文字，例如《莎士比亞全集》。」照這個定理，用香蕉請猴子，還是有機會打出想要的程式碼，對吧！

別說《莎士比亞全集》了，就算讓猴子在只有26個字母加一個空白鍵的打字機上，要能打出「to be or not to be」的機率就是1/(27^18)，機率已經極小了，無限猴子定理要追溯其最初的來源，其實想表達的是：當一件事發生的機率小到微乎其微時，可以當作不可能發生（可參考〈什麼都有可能發生？無限猴子定理〉）。

然而，一隻猴子不可能，那麼，一群猴子呢？例如，有位開發者Jesse Anderson從2011年8月開始，使用Amazon EC2、Hadoop和Ubuntu Linux，以數百萬隻虛擬猴子，隨機產生ASCII字元模擬按鍵，結果還真的重現了《莎士比亞全集》（可參考〈A Few More Million Amazonian Monkeys〉）。

雇主們看到這個結果，可別就這麼高興地把買香蕉的錢省下來，去買一堆機器與虛擬猴子了，因為，Jesse Anderson可是有著個明確的目標《莎士比亞全集》，如果沒有已經正確運行的程式碼作為目標，我們要怎麼知道百萬隻虛擬猴子打的程式是正確的呢？

世代傳承的程式猴

如果有一群虛擬猴子，子子孫孫都在打程式，我們給予一組繁衍規則，在數百甚至數千代之後，這群猴子可以打出什麼程式呢？如果有種程式語言可以用print helloworld，在螢幕顯示helloworld，並有個演算法實現了繁衍規則，讓某代中某隻猴子打出了print helloworld，那麼，就可以用來驗證演算法的正確性。

基因演算法可以是這類演算法之一。以虛擬猴子為例，若每隻猴子的基因隱含打某個鍵的傾向，16個基因組成了染色體，基因排列順序就是打字順序，例如，第一代會有一群猴子，每隻猴子的16個基因值是隨機的26個字母或空白，在這群猴子生存的虛擬世界中，打出的程式越接近print helloworld，適應度越高，越能得到配對繁衍的機會。

在繁衍下一代時，類似現實世界中的生物，會交換父母的基因來創造下一代的基因，例如，被配對的猴子的基因，若分別是paddfgqekoxdxllw與abgxhxhelkxtorld，最簡單的方式是各取前半段與後半段，得到paddfgqelkxtorld作為下一代的基因，這時有5個基因符合了目標，適應度更高了一些，讓這隻後代繼續繁衍，子孫打出正確程式的機會就更高一些。

有沒有可能一開始的初始猴子，基因全都不含print helloworld的任何字元呢？或者在順序上位置都不正確？有可能！這種情況下無論如何繁衍、交換基因，都不可能產生能打出print helloworld的後代，為了避免這類情況，可以令基因有突變的機會，例如，要求每個基因，可以隨機產生一個數字，若數字小於突變率，就隨機地用某個字元替代該基因。

令人驚奇的是，200隻虛擬猴子在數百或上千代的循環之後，真的有猴子能正確地打出print helloworld，而就現代電腦來說，這不過是幾十秒的時間。這樣的做法說穿了是碰運氣，不斷地試誤，對虛擬猴子來說，就是個「to be or not to be（生存還是毀滅）」的問題；但是，也不全然只有運氣，畢竟生存的世界有其規則，在規則的限制之下，讓生命自己找尋出路……呃……也可能沒有出路！

概觀基因演算法

從程式猴的例子中，我們可以看到基因演算法的幾個基本步驟。首先是將問題要處理的資料「編碼（Encoding）」為一組基因，也就是染色體（Chromosome），就上例而言是一組字串，就其他問題而言，可能是火箭力各推力的向量、遊行者造訪的城市座標等；接著是「初始化族群（Population）」，一開始必須產生適當數量的個體，這時個體的基因組合是隨機的，個體數量對求解有很大的影響──過少的話，子代難以多樣化，過多的話，會造成系統負擔等問題。

然後，來是進行「選擇（Selection）」，個體的適應度要設計適應函式（Fitness function）來計算，上例可以是每個基因與print helloworld符合的字元個數，然而，並不一定要使用基因作為輸入來計算，例如，可以是火箭目前位置與目標間的距離長度，或者是遊行的各城市間的總路徑長度，這部份是基因演算中最關鍵而困難的部份。

適應度值高的個體會被挑選至至交配池（mating pool），但通常不會只挑選菁英（例如只挑選適應度值前50%的個體），因為低適應值的個體可能含有關鍵基因。此時，比較好的方式，是使用幸運之輪（Wheel of fortune）之類的機率方法，也就是讓適應度值高的個體有比較高的機率被挑中，值低的個體被挑中的機率雖然比較小，然而還是有機會被挑中。

再來是「繁衍（Reproduction）」，從交配池中挑出的一對個體，進行基因交換的過程稱為交配（Crossover），上例是單點交配法（one-point crossover），實際上交換的點不一定是中間，可能是基因組中隨機的位置，或是在每個位置丟硬幣──若有個體A、B，正面選擇A該位置的基因，反面就選擇B的基因；依不同的情況，也可以選擇雙點、多點交配、均勻分配等方法。

突變（Mutation）是為了增加多樣性，就求解而言，是為了交配過程中，遺漏或缺少了關鍵基因，因而落入局部最佳解而非全域最佳解。突變率對於求解也有很大的影響──過小的話，補足關鍵基因的機會不多，過大的話，又會令適應高的基因流失，兩者都有可能造成求解過程成了單純的機率問題，而不是讓有優秀的基因傳承至下一代。

黑盒子求解最佳化

基因演算法適用於求解空間過大，難以在時間、資源等限制下求出的問題，乍看很像個黑盒子，因為無法知道整個族群的演化過程，只知道給一組參數，希望得到最接近目標的結果，例如，維基百科〈基因演算法〉條目中談到，日本新幹線N700系列車的車鼻，就是以基因演算法盡可能找出的風阻最小之車頭結構。

如果對基因演算法的實作有興趣，建議參考〈The Evolution of Code〉，其中使用Processing實作了幾種基因演算，除了打字猴的範例外，還有火箭、生物尺寸的模擬，這裡是個極為簡明的參考資源！