你不知道的費氏數列

踏入程式設計領域的初學者，應該都知道費氏數列（Fibonacci numbers）吧！最初，這是來自歐洲數學家Fibonacci在1202年發表的《Liber abacci》提到的「兔子算術」，若兔子每月生一隻小兔，一個月小兔又投入生產，那麼，每個月的兔子數量，會是1、1、2、3、5、8、13、21、34、55、89……

初學者總會在某文件或書中，練習如何透過程式碼產生費氏數列。最簡單的實作方式，通常有兩種：迴圈解或遞迴解，然後文件或書可能還會提到費氏數列是大自然的密碼，除了兔子以外，鳳梨、向日葵、鸚鵡螺等，生長過程或型態都隱藏著費氏數列。

舉例而言，樹枝成長若每個月分出一根樹枝，一個月新樹枝也投入生產，那麼，一開始是一根樹枝，一個月後就有兩根樹枝，二個月後有三根樹枝，三個月後有五根樹枝……，若將分支連接並繪製，就可以模擬樹枝成長的過程。

初學者應該也聽過巴斯卡三角形，將巴斯卡三角形靠左對齊（比較好觀察罷了），以右上左下方向畫出箭頭，箭頭遇到的數字加總，從上而下就會構成費氏數列，以圖片來呈現的話，可參考〈巴斯卡三角形〉。

另一個例子是黃金矩形，它可以由許多大小不同的正方形組成，而正方形的邊長關係，就符合費氏數列，而黃金螺線可以將黃金矩形中每個正方形的兩個對角，使用圓弧連接起來構造，其圖片的呈現，可參考維基百科〈Fibonacci number〉條目。

黃金矩形令人想到黃金比例，如果某個費氏數除以上一個費氏數，比例會接近1.618，也就是黃金比例，而越大的費氏數相除，會越接近這個數字；相對地，黃金比例的倒數，六就是某個費氏數除以下一個費氏數，比例會接近0.618，也就是黃金分割比，它是最難以有理數逼近的無理數。

費氏Q-Matrix到公式解

想產生費氏數列，雖然可基於Fn=Fn-1+Fn-2以迴圈或遞迴來實作，遞迴解適合用來理解分而治之的概念，然而會有重複計算費氏數的問題，太沒效率，迴圈解的時間複雜度則是O(n)；其實也可以基於矩陣，若從F0、F1開始計算，矩陣解的公式是：

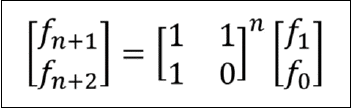
元素為1、0所組成的那個矩陣，稱為費氏Q-Matrix，現在這個問題就變成了矩陣的n次方問題了，程式實現時，可單純地實現矩陣次方演算，或者參考數的〈快速冪〉，來實現矩陣的快速冪演算，基本上時間複雜度會是O(log(n))。

如果你熟悉線性代數，應該知道這時候可以試著去求得特徵值（eigenvalues），以及特徵向量（eigenvectors），進一步求得矩陣的n次方，特徵值裡會含有黃金比例(1+√5)/2，而在特徵向量裡，也會有黃金比例的成分，進一步推導的話，就會得到費氏數列的公式解。

既然是公式，想求Fn不就是O(1)了？可惜的是，公式中會用到√5，單純就數學計算而言，雖然沒有問題，然而，在程式中，若只是用sqrt(5)之類的方式來求√5，估且不論sqrt本身演算就不是O(1)這件事，由於√5是個無理數，sqrt(5)的結果與真正數學上的√5是有誤差的，如果n很大，公式運算後誤差也會被放大，某個n以後就會得到不正確的數字。

當然，可以進一步透過BigDecimal之類的演算，使用更高的精度來解決問題，然而，這並不是沒有代價，因為這需要額外的空間，也需要額外的運算步驟，換言之，如果我們想以公式解實現費氏數列，必須視需求來衡量是否真的有效率。

費氏搜尋／費氏晶格

費氏數列可以用於資料搜尋演算，出發點就像二分搜尋，每一次都將搜尋區間分為兩邊，只不過並非對半切分，而是基於費氏數來決定切分位置，如果最初索引位置是Fn，該位的數大於指定搜尋值時，就往左找，小於時就向右，然而，尋找時的下個間隔會是Fn-1，這意味著每次搜尋都會基於費氏數來不斷切分，可想而知地，搜尋時的區間收斂速度更快。

初看費氏搜尋的演算過程，可能會摸不著頭緒，並且懷疑這種切分方式，難道不會遺漏元素嗎？此時，我們可以先試著理解費氏樹，它是個二分樹（binary tree），若任意節點值為Fn，n為大於0的數，如果n為1，沒有子節點，若n大於1，左子節點為Fn-1，右子節點為Fn-2。

如果保留費氏樹結構，先忽略節點值，只考慮末梢節點值與父節點值的差距絕對值為F1，每往上一層就以下個費氏數作為差距，然後從最左下的節點值為1開始（這是為了便於計算，被搜尋的數列索引從1開始），由下而上、由左而右地加上差距值來作為節點值，每個節點值就是費氏搜尋樹使用的索引，關於這部分的關係，可參考〈費氏搜尋〉的圖解，將搜尋過程整理為演算公式，過程中只需要用到加、減，不需要除法，在某些CPU比較有效率。

若將費氏數列做點變化，可以用於在球面上取得均勻點分布，所謂的均勻，是指每個點與點之間的距離相差不會太大（畢竟只有五個柏拉圖多面體，點與點之間才是真的等距），稱為費氏晶格（Fibonacci lattice）演算。

想理解球面的費氏晶格演算，我們可以先從圓的費氏晶格演算開始，若使用角度，可以將360乘上黃金分割得到黃金角（Golden angle），如果需要在半徑radius的圓內需要n個點，黃金角為θ，第i點座標就會是(radius/n*i*cos(i*θ), radius/n*i*sin(i*θ))，而這些點就像是某些植物的花瓣，或者向日葵的花蕊分布。

球面的費氏晶格演算，則是在每次旋轉黃金角前先增加高度，而產生的分布會像鳳梨紋路。為什麼要使用黃金角呢？因為它與黃金分割有關，基本上，黃金分割是最難用有理數逼近的無理數，也就是最以使用分數逼近的數，如果你希望在旋轉時儘量找到不重疊的角度，乘上黃金分割的黃金角是適當的選擇，有些植物可能只是想找到，能容納最多細胞的成長方式，自然而然地，就產生了像是費氏晶格演算的過程。

你可以在〈Evenly distributing n points on a sphere〉，找到圓或球版本的費氏晶格演算說明，以及Python實作。

大自然的密碼

費氏數列的應用非常多，在許多場合中，我不經意地都會發現費氏數列，例如，費氏晶格、L puzzle、五芒星的邊長關係等，我也曾經運用費氏數列做過不少的應用，無怪乎過去的數學家們，甚至成立過費氏學會，創辦過《費氏季刊》。

此外，我也收集、整理了一些費氏數列的相關文件，有興趣的人可以參考。你可以從〈費氏數列〉這篇文件開始，方才談到的費氏Q-Matrix、公式解、費氏搜尋等，該文中都有更多的圖解與說明，可從中體會費氏數列的奧妙。